ゲームに近い動きをさせる

６ゲームに近い動きをさせる（Stagingの応用）２

6.3 物体の微量な移動と、現在位置

(前回学んだように)物体(描画オブジェクト)を滑らかに移動させるためには、loopの中で、
translate:Unit メソッドを呼ぶ。
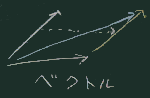
- と現在位置から指定された値（x方向、y方向、またはPointで移動量を指示する）だけ移動する。
ベクトル
描画オブジェクトについて、現在位置を求める単一のメソッドは用意されていない。
- 代わりに、origin:Point と offSet:Point の値を加算することで得られる。
  （どちらのメソッドも括弧をつけない）
- なおPoint型は相互に加算・減算ができる（結果の型もPoint型）。
  高校の数学Bで習ったベクトル（Vector）と同じと考えていい。

極座標

6.4 座標計算の基礎

直交座標

平面上の座標の表し方は、以下の２種類がある
（高校数学では主に前者のみ扱ってきている）。
1. 直交座標：原点（基準点）から、直交する２つの方向（x, y で表す）への偏移量の組
2. 極座標：原点（基準点）からの距離と、方向角の組
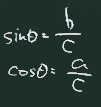
極座標から直交座標への変換は以下のように行う。
```
  def pol2ort(dist:Double, ang:Double) =
      Point(dist*math.cos(ang), dist*math.sin(ang))
```
pol2ort関数
- この pol2ort という名前は、右図のように、 pol(polar=極座標）から ort(orthogonal=直交座標）への変換という意味で、
  接続のための前置詞 to の代わりにそれと（英語で）同じ発音の two( = 2) を使って命名している（プログラミングではこういう命名がよく使われる）。
- ここで（高校数学でも習った）sin, cos, tan といった三角関数が必要となり、kojo ではそれぞれ、
  math.sin, math.cos, math.tan という呼出し方をする。
また、直交座標から極座標（を構成する各々の値）は以下のように計算できる。
```
  def polDir(to:Point, from:Point):Double=
      math.atan2(to.y-from.y, to.x-from.x)
  def polDist(p1:Point, p2:Point):Double=
       math.sqrt(math.pow(p2.x-p1.x, 2) + math.pow(p2.y-p1.y, 2))
```
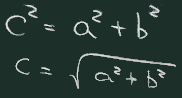距離の計算
- 直交座標で座標値を表す２つの数値の対はPoint型でまとめて表現できるが、それに対して、
  極座標で座標値を表す２つの数値をまとめて扱う型は（kojoでは）用意されていないので、別々の式で求める。
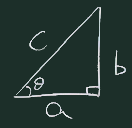
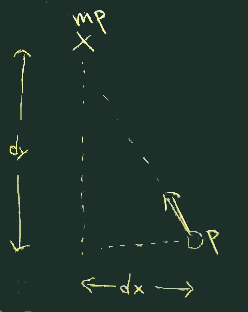
- 距離（distance -> dist) は、ピタゴラスの定理に基いて求めることができる（右図）。
- 角度を求める時は、tan（タンジェント)の逆関数である arctan（アークタンジェント）を用いる。
- arctanは以下の式（下左図）で与えられるが、実際には tanの値は下中図のような形で、 b（x方向）の値が0に近づく 90°、270°の近辺で ±無限大に発散する（コンピュータでこの計算をさせると「除数0で割り算をした」というエラーになる）。
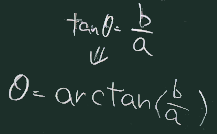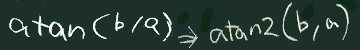- そのため、a, b の２つの値を（除算をせずに）引数として渡して arctanの計算をするための関数 atan2 が（数値計算のできる殆どの言語で）用意されている（下右図）。
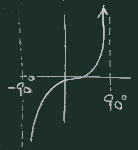
tanの定義 tanのグラフ atan2

6.5 物体に、手駒を追跡させてみる

追跡

それぞれの物体を基準点としたときの、手駒（プログラム例では me）を望む位置（極座標）を求め、
その方向に向けて、適当な偏移量だけ移動(translateメソッド)させる。
偏移量は距離に対する関数として記述するのが一般的だが、その値の定め方としては、以下のように様々な可能性がある。
1. 一定量。
2. 距離に比例した速さ：距離に0以上1未満に定数を掛ける。
3. 近いほど速い（重力運動をシミュレートすることになる）：
  例えば適当な定数を距離で割った値など
  （ただし接近しすぎの時に異常な動作をすることがあるのでそれを防ぐ工夫は必要）。

以下の例は 3. に沿って計算したもの。

  def speed(orgn:Point, tgt:Point):Double= {
      val d = polDist(tgt, orgn)
      if(d < 40) 0 else math.min(3, 300/d)
  }

loop の中で、以下のような処理を行うことになる。

  val mp = mousePosition
  me.setPosition(mp.x, mp.y) // 6.1 の別の書き方
  for (c <- cs) {
      val p = c.origin+c.offset
      c.translate(pol2ort(speed(p, mp), polDir(mp, p)))
  }

ここまでの補足と実演例

6.6 （参考）forを使わない書き方

（第10回での実演にも含まれていたが）以下の２つには、別の記法（メソッド呼出による）が用意されている。
1. for　を使った繰り返し実行
2. for + yield （内包表記）を使ったデータの集合体の生成
実際には forによる書き方が、メソッド呼出による記法の「糖衣構文」（Syntax Sugar）として作られている。
for の後ろの括弧内の矢印（<-）の右辺に、繰り返しが可能なオブジェクトやデータ構造（「Iterableインタフェースを実装したクラスのインスタンス」）が置かれるが、
そのオブジェクトに対するメソッドが多数用意されている。

内包表記： map に変換される

 for(i<-1 to 20) yield s.circle(...)
 // ↑ と ↓ は 同じ意味
 (1 to 20).map{(i)=>s.circle(...)}
 (1 to 20).map((i)=>s.circle(...))
 (1 to 20).map(i=>s.circle(...))
 1.to(20).map(i=>s.circle(...))
	
 // ちなみに 以下の２つも同じ意味
 1 to 20
 1.to(20)
 // だが、
 1 to 20.map(...)  // これは使えない（括弧がないと意味が変わるため）

繰り返し実行： foreach に変換される

 for(c<-cs) { ... }
 // ↑ と ↓ は 同じ意味
 cs.foreach(c=>{...})

6.7 （物体にとっての）危険地帯を作ってみる

四角い枠を作る

 val trap = s.rectangle(-50, -30, 100, 60)
 trap.fill(rancol)

その中に入る物体を検出する

 cs.filter(c=>{
     val p=c.origin+c.offset
     p.x<50 && p.x>-50 && p.y<30 && p.y>-30
 })

6.8 物体の消去

hide すれば画面からは消える
が、オブジェクトのCollection （上記リストでは cs）　　の中には残っているので、取り除く必要がある。
データに変化を引き起こすとき、以下のいずれかの方法でデータの（変化に対する）性質を変えておく必要がある。
1. val でなく var変数を使い、元のCollection から該当する要素を取り除いた新しい Collection を生成させて、変数に（新しい値として）セットする。
2. mutableな（その逆の immutable だと変更を受け付けない）Collectionを使い、
  要素を削除するメソッドを呼ぶ。
  （こういったメソッドは「破壊的」メソッドと呼ばれる）
当該オブジェクトへの参照（変数やCollectionから到達できる状態）がすべてなくなった時点で、プログラムの中からもそのオブジェクトは消滅する。
- そのオブジェクトが占有していたメモリ上の空間も返却され再利用にまわせれる。

6.9 物体の残存数をカウントし、不足分（の一部）を補充

Collectionに含まれる要素の数は、以下の方法で求められる。
```
  cs.length
```
（参考１）ある条件を満たす要素の数を求めるには、以下のように書くことになる。
```
  cs.filter(c=>{...}).length
```
- このように、メソッド呼出の結果の値に対してさらにメソッド呼出を行うプログラミングの流儀を「メソッドチェーン」と呼ぶ
（参考２）要素の数を求める書き方は他にもある cs.reduce((r,v)=>r+1)
- reduceメソッドの使い方は次回あらためて扱う予定


tanの定義	tanのグラフ	atan2

６ ゲームに近い動きをさせる（Stagingの応用）２

6.3 物体の微量な移動と、現在位置

6.4 座標計算の基礎

6.5 物体に、手駒を追跡させてみる

6.6 （参考）forを使わない書き方

6.7 （物体にとっての）危険地帯を作ってみる

6.8 物体の消去

6.9 物体の残存数をカウントし、不足分（の一部）を補充

６ゲームに近い動きをさせる（Stagingの応用）２