再帰（関数の再帰呼出）について

• 関数 xxxの中で 自分自身 xxxを呼び出す使い方
• 英語では recursion （～recursive)
• 探索等に有効
• 油断すると無限再帰をしてしまうので注意

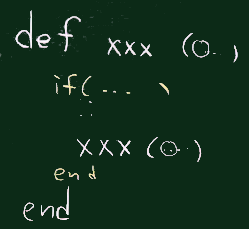
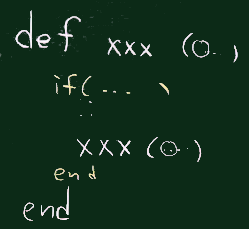
有効な再帰の条件

1. 末端があること（末端では再帰しない）。

2. 呼び出し１レベル毎に末端に向けての変化があること。

3. 変化の経路がループになっていないこと。

   （ループの可能性のある経路はチェックして踏み入れない）

   • 無限に再帰呼び出しが行われると一般には 「スタックオーバーフロー」を引き起こす。

   （関数呼出のときに戻るべきアドレスや呼出元の 途中経過がスタックに「積まれ」、それがスタックとして 用意されたメモリ領域からあふれることによるエラー）

   • 現在のRubyでは

      SystemStackError: stack level too deep

     という表記になるが意味は同じ。

   • スタックオーバーフロー、はプログラミングの世界では有名なフレーズなので、ずばりその名前のサイト（Q&Aのサイト）まである状態。

• 再帰を使わない場合でも無限ループになるプログラムは 簡単に作れる（作れてしまう；右図）。
  • 一般的には Ctrl-Cで強制停止できるのでそれを さほど恐れる必要はないが（製品としてのプログラムに 無限ループが発生すると大問題だが）。

再帰の例

1. 階乗の計算 （英語で factorial)

   数学で用いられる帰納的定義（概ね右図のような）に沿って書くとこうなる：

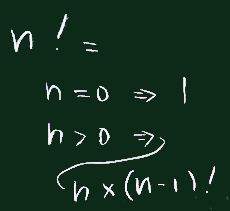
   def fact(n)
      if n <= 1 then 1
        else n*fact(n-1)
      end
   end

   

   • 前述の条件を確認しておく。

     1. 再帰では 呼出しの深さが１段深くなると、

        末端に向けて一歩 近づく 　 　 （fact だと n が１つ小さくなる）。

     2. 終端の条件： 1! = 1 => n が1なら 再帰呼出はしない。

   • 注）Ruby（などの高階関数のある言語）では階乗計算は再帰を使わないで書かれる傾向がある。

     • 前回の文字列を整数に変換するコードと同じ考え方で、以下のように実現する。

       (1..n).reduce(:*)

     • 論理の組み立て方は右図のように再帰と演繹（えんえき）に分類される。
       

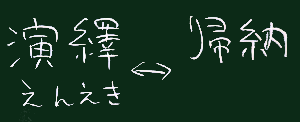
• プログラミング界では「末尾再帰(tail recursion)」の形のものが好まれる。

  末尾再帰では、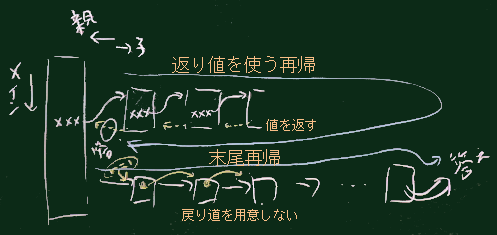 　

  • 親（呼出元）は子（呼出先）の終了を待たず、 　 - 末端で最終的な答えを出す。

  def fact(n,r=1)
    if n <= 1 then r
      else fact(n-1,r*n)
    end
  end

2. アッカーマン関数 （再帰の例として有名）:

   • ack.rbを参照（およびためしに実行）されたし。

   • 実行の方法

     ack.rb 3 3 2

     など。

   • x y の値（第1 第2パラメータ)で実行回数が決まるが、

     値（特にx)が大きいと 爆発的に回数が大きくなる。

     • （4以上の値で実行させるときは要注意（なかなか終わらない）。

3. 他に フィボナッチ数列 たらいまわし関数（竹内関数とも呼ばれる）も有名

4. 前回課題の、整数を文字列に変換するコードの例も提示しておこう。

   

   def n2s(n,r="")   # nは0以上の整数 を前提としておく
       if n<=0
           then (r==""?'0':r)
           else n2s(n/10,'0123456789'[n%10]+r)
       end
   end

   おまけ

   (m <- 2..16 についてのm進数に拡張；基数mを第二引数で渡す）

   def n2s(n,rdx=10,r="")   # assume rdx(raddix) <=16
        if n<=0
            then (r==""?'0':r)
            else n2s(n/rdx,rdx,'0123456789abcdef'[n%rdx]+r)
        end
    end