エラトステネスの篩

素数生成の方法いろいろ

素数を生成するプログラムの作り方はいくつかある。 （なお、素数については「プログラミング 小手調べ」でも扱っているので参照されたい。）

1. 整数の集合を用意して、２の倍数、３の倍数、…を順に消していく。

   (2..Math.sqrt(n)).
     each_with_object(a=(2..n).to_a){|i|
       (2..n/i).each{|j|a.delete(i*j)}
     }

   • ４の倍数、６の倍数など冗長なチェックもしてしまい非効率、
   • 範囲を決めての素数列生成しかできない、といった欠点があるだろう。

2. （まずは有限の）整数列を用意して、前から順に取り出して、 既知の素数列で順々に（割り切れるか）チェックし、 通過したものを新しく既知の素数列に加える。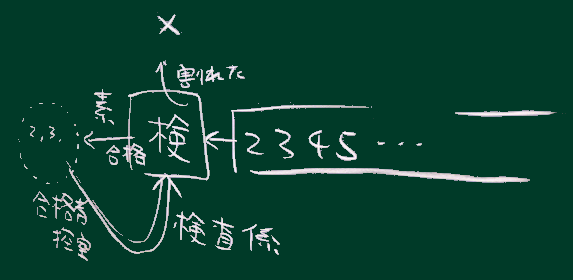

   （考え方としては右図のように待機列から順々に取り出すイメージになるだろう）。

   • チェック係となる既知の素数の値の範囲は、 チェック対象の数の平方根以下に限定してもいい （% の演算の回数は半分以下に減らせる）。

   • チェック係（除数）は小さい数のほうが割り切れる （即ちチェック対象が素数でないことが判明する）確率が高いので、小さい方を優先的に（昇順に）適用するのがいいだろう。

   • Rubyで書いてみる

     # 有限整数列バージョン
     def sieve(mx)
       (2..mx).reduce([]){|p,i|
         sq=Math.sqrt(i)
         p.take_while{|j|j<sq}.
           find{|e|i%e==0}    ?p:p+[i]
       }
     end
     sieve(100)     # など

   • JS版

     function sieve(mx) {
        let primes=[]
        for(i=2; i<=mx; i++){
            sq=Math.sqrt(i)
            primes.filter(e=>e<sq).
            find(e=>i%e==0) ||
            primes.push(i)
        }
        return primes
     }
     sieve(100)         //など

   • CoffeeScript（JSとRubyの折衷のような）版

     sieve=(mx)->
       [2..mx].reduce(((a,i)->
         sq=Math.sqrt(i)
         if a.filter((e)->e<=sq).find((e)->i%e==0) then a else [a...,i]),[])
     console.log(sieve(1000))

   • Python版も

     import math
     def sieve(mx):
       primes=[]
       for i in range(2,mx):
         sq=math.sqrt(i)
         p1=list(filter(lambda x:x<sq,primes))
         p2=list(filter(lambda e:i%e==0,p1))
         len(p2)>0 or primes.append(i)
       return primes

   • pythonの使いづらさを改良したcoconutという言語もある（が、以下の例ではその便利さはわかりづらいかも知れない）。

     import math
     def sieve(mx):
       primes=[]
       for i in range(2,mx):
         sq=math.sqrt(i)
         primes|>\
         filter$(x->x<sq)|>\
         filter$(e->i%e==0)|>\
         list|>len > 0 or primes.append(i)
       return primes

3. 無限整数列からスタートすることもできる（言語によって書きやすさがだいぶ変わってくる）

   • 最もシンプルなのはこれだろう

     sieve (n:ns) = n:sieve(filter(\k->k `mod` n/=0) ns)
     take 100 $ sieve [2..]

     • 12/21 訂正 filter関数の中のラムダ式で演算`mod` の左辺と右辺(kとn)が逆になってたのを訂正しました
     • なお、ここではfilter関数を使っているが、前述の 「小手調べ」では、「リスト内包表記」を使った例を提示してある（どちらを使っても構わない）。

   • Scala でも、遅延評価ができる

     object Primes {
       val primes = sieve(Stream.from(2))
     
       def sieve(st: Stream[Int]): Stream[Int] = {
         val x = st.head
         x #:: sieve(st.tail.filter(_ % x != 0))
       }
     
       def main(args: Array[String]): Unit = {
         println(primes.take(10).map(_.toString).reduce("%s, %s".format(_, _)))
       // => 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
       }
     }
     // from https://hotoku.hatenablog.com/entry/20150122/1421889166