初歩的な電卓（３）

６初歩的な電卓（３）

6.6 構文解析をしてから計算を実行させる

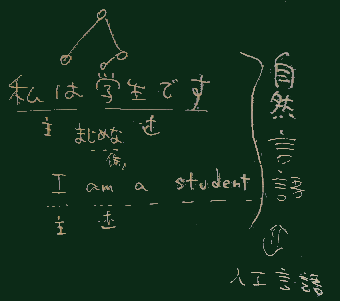
全体の流れ

scan() ->[トークンのリスト] -> parse() -> [構文解析木] -> calc()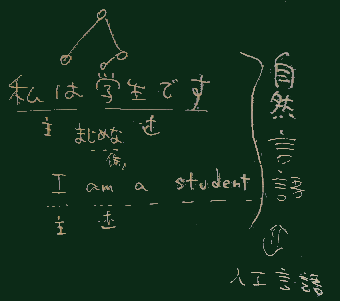

補足1 構文解析について

自然言語（日本語や英語など）でも、それを理解するために構文解析（parsing）は行われる。

補足２解析木の概要

数式を解析した木の場合、下図のような形のものができる。

演算子が節点（node）を構成する（右図）
数値（被演算子）が葉（leaf）となる。
なお、（解析木を含めて）コンピュータ科学では木を描くときは根を上に書く慣習がある
木構造のデータは、モデルとしては上左図の上半分のように認識されるが、プログラム内では、適切なデータ表現で表す必要がある。
- しっかりしたプログラムでは節点を表現するクラスや構造体を設計するのだが、
- 今回は勘弁なデータ構造として（上左図の下半分のように）タプルで表現することにしておく。

構文解析の考え方１

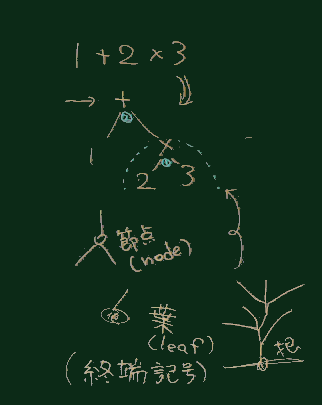
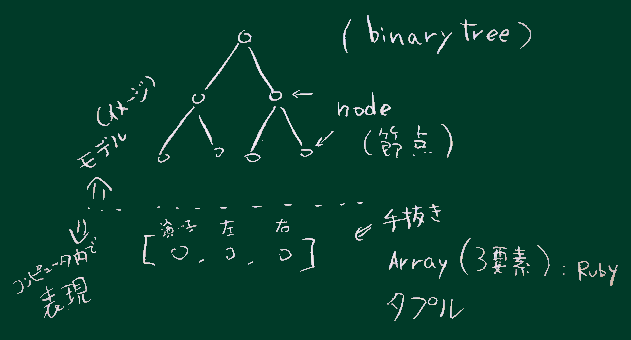
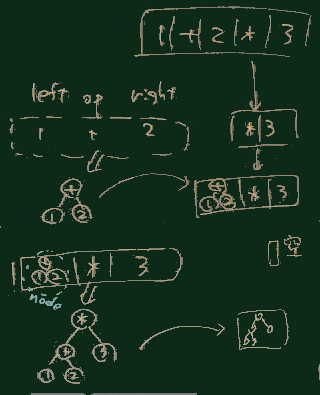解析１（即時計算の時と同じ考え方）

以下を繰り返す
   トークンリストから、left op right の３つを取り出す
      取り出したものが left だけであれば繰り返しを終了
   ３つをノードとして１つのデータ（ここでは配列）にまとめ、
    トークンリストの先頭に書き戻す

プログラムとしては以下のような形になる

while (left, op, right = tokenList.shift(3)) and op do
    tokenList.unshift [op, left, right]
end
p left  # ここに構文木が作られている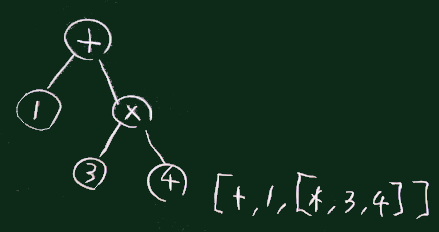

上記の方法で解析すると右上図のような構文木になる。
同じような式（ここでは「1+3*4」）を数学のルールに沿って構文解析すると、右下図に示す構造になる。
- 結果の形の違い（と意味の違い）を確認されたい
- ここでは１つのノードをRubyのタプル（３つ組；Arrayで実現）で表すので、結果のデータ（をRubyで表示したもの）は図の右下のリストのようなものになる。
なお、上のコードで、whileの右、多重代入をしている式を囲む括弧 () を省略すると文法エラーが発生する。多重代入でない単純な代入だと、演算子 = が and よりも優先度が高いので ()は省略できるが、なぜか多重代入については差があるようだ。

構文解析の考え方2

この形ではプログラムに発展性がないので、トークンを１つずつ取り出して処理するプログラムにしてみる。（ただし数式の文法違反の検出は当面は行わない）

トークンリストから予め１つ取り出して left に置いておく
トークンリストから１つずつトークンを取り出して以下の処理をする
   トークンが 演算子ならば op に置いておく
   トークンが 数値ならば、（そのトークンを最新トークンとすると）
        op left 最新トークン でノード（構文解析木のノード）を作り、
        left に置いておく

構文解析の考え方3

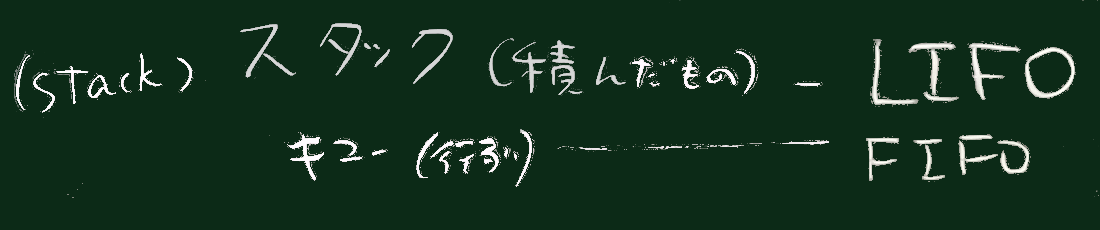先のプログラムでは変数を２つ（left, op) 使った（rightはすぐに消費するため使わなかった）が、代わりに、スタック（LIFO型の１次元データ構造）を使う。

スタックは、rubyではArrayで実現できるが、
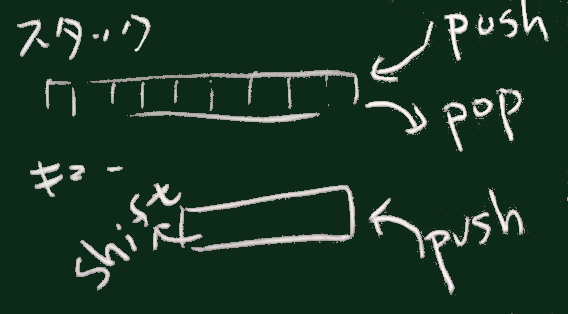
push, pop の２つのメソッドだけを使う（ここでは、プログラムを作る人がその制限のもとにコーディングする）。

すなわち、Arrayの末尾側の末端でのデータ出し入れだけを行うことになる。
スタックのイメージ

a=[] ; a.push tokenList.shift
while t=tokenList.shift do
    case t
    when Symbol then a.push t
         # 演算子はスタックに積む
    when Numeric
         a.push [a.pop, a.pop, t] # ３つ組を積む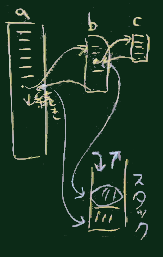

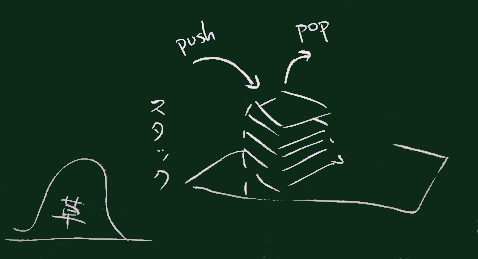
なお、スタックは、右図のようにプログラム（メインの流れ）から関数（サブプログラム）が呼び出されるときに、戻り先（を含めて作業途中の状態）を保存しておく場所として広く使われている。
スタックのLIFO的動作のため、関数呼出が２段３段にまたがっても、関数実行終了時に正しく戻れることが担保されている。
- （参考として）プログラミング言語処理系でのスタックの使われ方を体感するためには、
```
def x()
  x
end
```
  といった（無限再帰する）プログラムを実行してみると、 Stack に関するエラーが発生することを見る事ができるだろう。
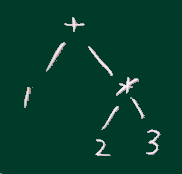
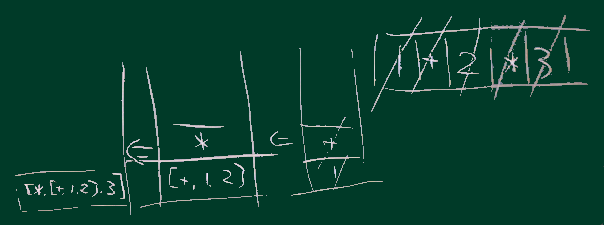
式 1+2*3 は、数学のルールに従うと右右図の木構造として解析されるべきだが、本項の方式だと右図のようなスタックの動きで ['*',1,['+',2,3]] になる。

2. 優先度のある数式を扱う

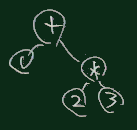（さらにしっかりしたプログラムにする）

優先度を考慮して構文解析を行うと、その結果の解析木は、これまで見た例とは違い、（考え方1の右図に示した式 1+2*3 に対して）右図の形になる。

以下のような手順で解析を行う。

トークンリストが空になるまで以下を繰り返す

とりだした先頭トークン tk が
  数字ならば、スタックにpush
  演算子ならば スタック[-2]にある演算子（op1と呼んでおく） を見て、  *
　 1 op1が空（nil）ならば
    tk を スタックにpush
  2 tkの優先度 > op1の優先度 ならば
    tk を スタックにpush
　 3 そうでなければ（ tkの優先度 <= op1の優先度 ）
    スタックから３つ組を取り出し  *
    ノードとしてまとめ、
    そのノードを再度スタックにpush した上で、
    最初に戻る
すべてのトークンを処理したら
    スタックから３つ組を取り出し、ノードとして再度push
    を繰り返す（３つ組が取り出せなくなるまで）

最後にスタックに１つだけ残った要素が、構文木を表すタプル（多重のタプル）となる。

解析過程でのスタックの状態の変化（黒板図）を別ページに示す。また、これを実現するプログラム例を以下に示す。

def parse1(tk,a)
  puts "#{tk} - #{a}"
  case tk
  when Numeric  then a.push tk      # 被演算子
  when Symbol then                  # 演算子
    if prior(tk) > prior(op1) then  # 優先度が高い => スタックに積む
      a.push tk
    else                            # 優先度が低い または同じ優先度
      l, op, r = a.pop(3)
      a.push [op, l, r]
      parse1(tk, a)                 # 再度呼ぶ（再帰）
    end
  end
end
def parse(tokenList)
  (tokenList+[:END]).each_with_object(a=[]){|tk,a|parse1(tk,a)}
  a[-2]
end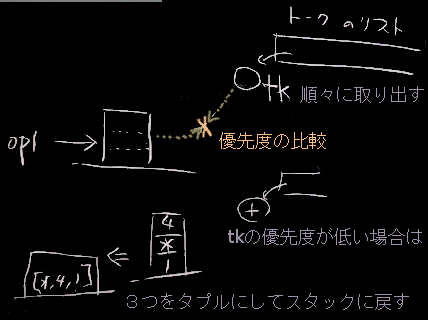

parse() はトークンの配列を受け取る。
parse() の中で、下請け関数 parse1() を（各トークンについて）呼んでいる。
ただしトークン配列の末尾に特殊なシンボル :ENDを事前に追加している。
parse1() の中で、「再度呼ぶ」の場面では、再起呼び出しを使っている。
スタック（最初は空）を用意する。配列として作り、上記例では、a という名前で引用している。
上記のプログラム内では、op1 は定義していない（説明の都合で名づけてある）ので、プログラムとして動作させるためには、これを a[-2] と置換えて下さい。（配列の最後から２つめの要素。ただし存在しなければ nilを返す）
トークンを前から順に処理するための、本プログラムの中心軸となる流れは、 each や map ではなく、each_with_object を使って構成しているが、これは変数 a に対する変更の範囲をこの流れの中に限定するため。

補足１再帰について

ある関数の中から、その（同名の）関数を呼び出すことを「再帰」呼び出しという（重要な概念なのでしっかり理解しておくこと）
不用意に再帰呼び出しをすると無限に連鎖してしまう可能性があるので注意が必要
上の例では、呼び出す毎にスタックaの長さが２ずつ減るので、いつかは、（スタック長が短いことにより）再帰呼び出しを行わない条件分岐に入るよう仕組んだ上での再帰呼び出しを行っている

補足２プログラミングのテクニック

op1が空の時の判断：
- 前述の手順（言葉で説明した版）では３分岐していたものを、プログラム例では２分岐ですませている
- これは、op1が空の時の判断をせず、その代わりに、op1がnilの時に（これを演算子だと仮定して後述のHashを使う方法で表引きを行って）それに対する優先度（を表す数字として、最も弱い数値である）-1 を返させるようにすることで代用できるからである。
- これをシンプルなコードで実現できるよう、Hash（後述）のデフォルト値を -1 に設定している。
後処理（前述の「すべてのトークンを処理したら」）の実現：
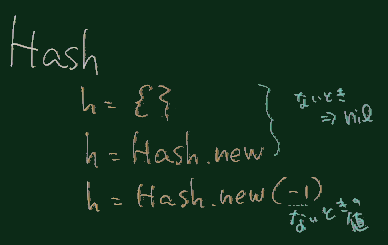
- 後処理をプログラムするとしたら、
```
l, op, r = a.pop(3)
a.push [op, l, r]
```
  のようなコードを、whileで繰り返すか再帰的に呼ぶか、という実現方法がある。しかし、
- このコードは、前述のコードで「# 優先度が低いまたは同じ優先度」の時と同じことをしている。
- 以下の方法で、この部分が後処理を兼用にすることも可能になる
  - トークンリストの最後に、ダミーの演算子を置き、
  - その優先度はどの演算子よりも低いものとして扱う
- そのために（ここでは :END と名付けた）特殊な疑似演算子を導入した。

3. 評価器

node は、３つの値のタプル（１つの演算を表す；配列で実現）または、終端子（数値）のいずれか。
評価器 val() は、再起的に呼び出される
終端子を受け取ったときはその値をそのまま返す。

タプルを受け取った時は、演算の左右オペランドをそれぞれ評価してから、その結果の値に対して所定の演算を行い、その結果を返す。

def val(node)
  case node
  when Numeric then node
  else
    op,l,r=node
    case op
    when '+' then val(l)+val(r)
    when '-' then val(l)-val(r)
    when '*' then val(l)*val(r)
    when '/' then val(l)/val(r)
    when '%' then val(l)%val(r)
    end
  end
end

4. 演算子の優先度判断

例えば以下のような実現方法がある
配列の形で優先度のリストを用意し、それを Hash（連想配列）に予め変換しておく。
演算子（シンボル）の優先度はそのHashを「引く」だけで実現できる
なお、文字列をシンボルにするためには記号 : を文字列に前置させる。（通常の文字列だとクオートする必要がないが ( ) = などの文字はクオートする必要がある）
```
def op2hash(list)
  h=Hash.new(-1)
  list.each{|e|n=e.shift;e.each{|o|h[o]=n}}
  h
end
OPERlist=op2hash([[0,:'(',:')',:END],[1,:'='],[2,:'+',:'-'],[3,:'*',:'/']])
def prior(op) OPERlist[op] end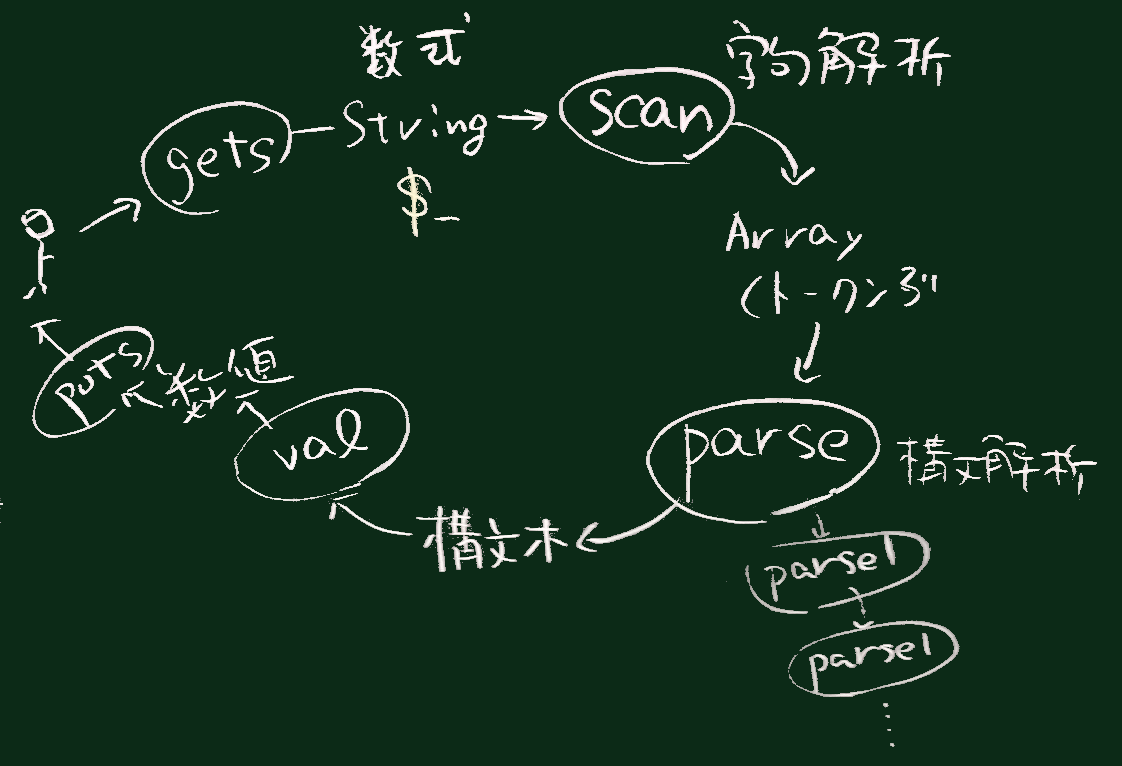
```

注）

前に示した構文解析のプログラム例ではトークン列の末尾に置いた偽演算子 :END が重要な役割を果たしている。
この :END の優先度を、nil に対する（デフォルトの）優先度 -1 と同じ値にすると、無限に再帰呼び出しをしてしまうことになる。
OPERlistに ：END を（nil よりも高い優先度で）設定しておく必要がある（上の例では 0に設定した）。

全体像

全体のデータの流れは右図の通り。

def scan(str)  # 数式を表す一行の文字列 str を受け取り
   ...
   # トークンの配列を返す
end

def parse(tokenList)  # トークンの配列を受け取り
   ...
   # 構文木を返す
end

def val(node)  # 構文木（を構成する１つのnode）を受け取り
   ...
   # そのnode（と下位node）を評価（計算）した値 を返す
end

### メインプログラム
while gets do
   puts val(parse(scan($_)))
end

６ 初歩的な電卓（３）